From ARCHICAD 21 a macro called BasicGeometricCalc has been added the ARCHICAD Library. As its name suggests, this macro contains basic geometrical calculations, which can come in handy for GDL 2D and 3D scripting.
With the introduction of DICT in ARCHICAD 23, the parametrization of BasicGeometricCalc has been renewed to use dictionary type parameters and return values in a new macro called BasicGeometry. BasicGeometricCalc is deprecated, only BasicGeometry is updated with new functions. Most of the previously existing functions work the same way with the same geometric data, but some functions of BasicGeometry return more detailed results, some functions have been added, and one function’s return value has changed (see table below).
The macro does geometric calculations. The required method should be given in the macro call with the input data belonging to it. The results of the calculation are given back as returned parameters from the call. It only uses the Master script so it can be called from 2D scripts and 3D scripts as well.
Feel free to save a copy of this macro with a different name, and use it in your own library packages. If any problem or question occurs regarding this macro, please notify us in a comment under this post or in the forum.
DICT structure documentation conventions
The various functions of the macro use dictionary structures. GDL doesn’t have types to identify dict structures, so we have to document the expected and returned structures. The following format is used:
name_of_parameter
.key
.subkey1 .subkey2 (type) comment
? .optional_key
.array[]
.subkey
Where parameter type is not written explicitly, it is a dict. Where key type is not written explicitly, it is a real number (floating-point value). Keys that have subkeys – marked with identation – are dict type.
The necessity/existence of optional keys depend on the values of other keys or input values.
The name of a returned parameter can be anything, we only give a suggestion that gives a hint to its meaning.
For example:
circle
? .specialPoints[]
.x .y
.center
.x .y
This means the following code is valid:
if haskey(circle.specialPoints) then
for i = 1 to vardim1(circle.specialPoints)
line2 circle.center.x, circle.center.y, circle.specialPoints[i].x, circle.specialPoints[i].y
next i
endif
Geometric concepts used by BasicGeometry
accuracy
- Vectors with both coordinates (absolute value) smaller than 0.0001 (1 / 10 mm) are considered null vector.
- Points with both coordinates closer than 0.0001 (1 / 10 mm) are considered the same point.
- Angles (absolute value) smaller than 0.0081° (1 / 10 mm divergence over 1 m) are considered zero.
direction vector
A vector that has length 1 (1 meter). It’s length can be changed easily by multiplying all it’s components by the desired length.
arc
A circular arc whose central angle’s absolute value is between (excluding) 0° and 360°. The sign of the angle is the same as the direction of rotation from the beginning point to the endpoint (see figure below at polygon).
segment
A line between two points that can be either straight or an arc. Defined by it’s two endpoints, type, and central angle for curved segment.
edge
A line starting from a point that can be either straight or an arc. Defined similarly to a segment, but omitting the end point. The endpoint is the beginning point of the next edge, thus an edge can’t stand on it’s own.
polygon
A collection of edges, without explicitly duplicating the starting point at the end.
The same as a closed polyline.
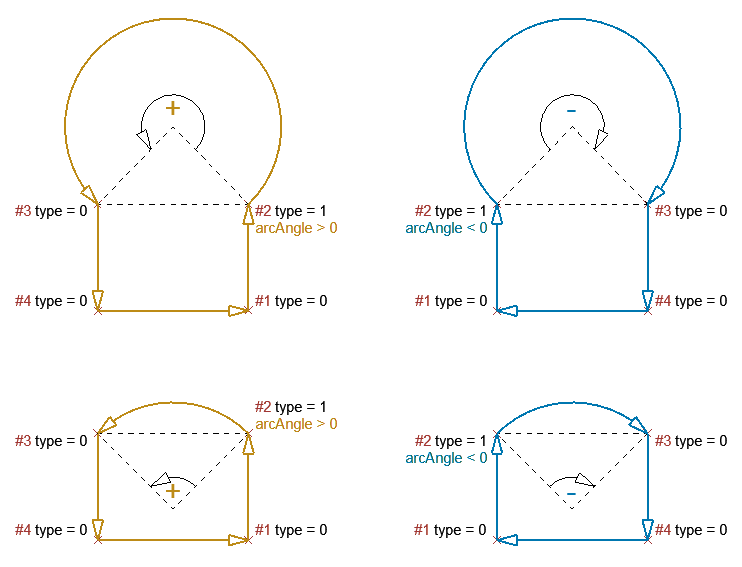
polyline
A collection of edges. It can be closed (the same as a polygon) or open: the endpoint can be different than the starting point.
An open polyline is defined by the same number of edges as a closed one, but the last edge is only needed for the endpoint of the polyline, its type is disregarded.
Functions
The function of the macro can be chosen by the iFunction parameter. The available values of this parameter are referred by named variables in the macro and in this post as well:
| description | space | iFunction | name in BasicGeometry | name in BasicGeometricCalc | changes in BasicGeometry |
| Direction vector between two points | 3D | 1 | BasicGeometry.DIRECTION_POINTS_3D | DIRECTION_POINTS | Returns whether input points are the same. |
| Vector mirrored across an axis | 2D | 2 | BasicGeometry.MIRROR_VECTOR_2D | MIRROR_VECTOR | – |
| Direction vectors of segment end points | 2D | 3 | BasicGeometry.DIRECTION_SEGMENT_2D | DIRECTION_SEGMENT | Returns whether input points are the same. |
| Intersection of two lines | 2D | 4 | BasicGeometry.INTERSECT_LINE_LINE | INTERSECT_LINE_LINE | Doesn’t return number of intersections explicitly. |
| Intersection of a circle and a line | 2D | 5 | BasicGeometry.INTERSECT_CIRCLE_LINE_2D | INTERSECT_CIRCLE_LINE | Doesn’t return number of intersections explicitly. |
| Intersection of a segment and a line | 2D | 6 | BasicGeometry.INTERSECT_SEGMENT_LINE_2D | INTERSECT_SEGMENT_LINE | Doesn’t return number of intersections explicitly.Returns tangents at intersections. |
| Intersection of a polygon and a line | 2D | 7 | BasicGeometry.INTERSECT_LINE_POLYGON_2D | INTERSECT_POLY_LINE | Doesn’t return number of intersections explicitly.Returns tangents at intersections. |
| Insert a point onto a segment at given distance from start | 2D | 8 | BasicGeometry.INSERT_POINT_TO_SEGMENT_2D | INSERT_POINT_TO_SEGMENT | – |
| Segmentation of an arc with given tolerance | 2D | 9 | BasicGeometry.SEGMENT_ARC_2D | SEGMENT_ARC | – |
| Intersection of two circles | 2D | 10 | BasicGeometry.INTERSECT_CIRCLE_CIRCLE_2D | INTERSECT_CIRCLE_CIRCLE | – |
| Intersection of a segment and a circle | 2D | 11 | BasicGeometry.INTERSECT_SEGMENT_CIRCLE_2D | INTERSECT_SEGMENT_CIRCLE | Doesn’t return number of intersections explicitly. |
| Distribute points evenly on polyline | 2D | 12 | BasicGeometry.DISTRIBUTION_POLYLINE_2D | DISTRIBUTION_POLY_LINE | Doesn’t return number of intersections explicitly. |
| Align Z with vector | 3D | 13 | BasicGeometry.ROT_Z_TO_VECTOR_3D | ROTANGLEZ_FOR_NORMVECTOR only available since version AC22 | Returned angle is measured at a different location. |
| Project points perpendicularly onto line | 2D | 14 | BasicGeometry.PROJECT_POINTS_LINE_2D | not available | – |
| Transform points | 3D | 15 | BasicGeometry.LOCAL_POINTS_TO_GLOBAL_3D | not available | – |
| Inverse-transform points | 3D | 16 | BasicGeometry.GLOBAL_POINTS_TO_LOCAL_3D | not available | – |
| Arc through three points in order | 2D | 17 | BasicGeometry.ARC_THROUGH_POINTS_2D | not available | – |
| Project points onto circle from inside | 2D | 18 | BasicGeometry.PROJECT_POINTS_CIRCLE_INNER_2D | not available | – |
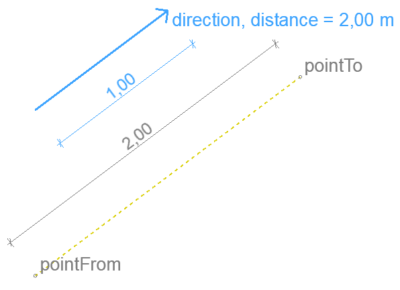
Direction vector between two points – 3D
Returns the direction vector from pointFrom towards pointTo, and the distance between them.
Input
pointFrom pointTo
.x .y .z
2D calculations can be done by setting z to 0.
Result
direction
.ux .uy .uz
? .is0 (bool)
distance (real)
Returns a null vector when the two points are closer than 0,00000001 (1 / 100 000 mm). The key direction.is0 only exists in this case, but distance is not necessarily 0.
Code snippet
dict _direction
call "BasicGeometry" parameters iFunction = BasicGeometry.DIRECTION_POINTS_3D,
PointFrom = _pointFrom,
PointTo = _pointTo,
returned_parameters _direction,
_distance
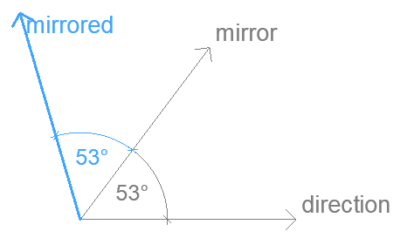
Vector mirrored across an axis – 2D
Mirrors a direction vector on an axis given by another direction vector.
Input
direction
.ux .uy
mirror
.ux .uy
Both input vectors should be direction vectors. This is not checked, but results will be incorrect if their length is not 1.
Result
mirrored
.ux .uy
Mirroring a null vector the result is a null vector.
Mirroring on a null vector axis is central inversion, the result will be the opposite of the input.
Code snippet
dict _direction dict _mirrored call "BasicGeometry" parameters iFunction = BasicGeometry.MIRROR_VECTOR_2D, mirror = _mirror, direction = _direction, returned_parameters _mirrored
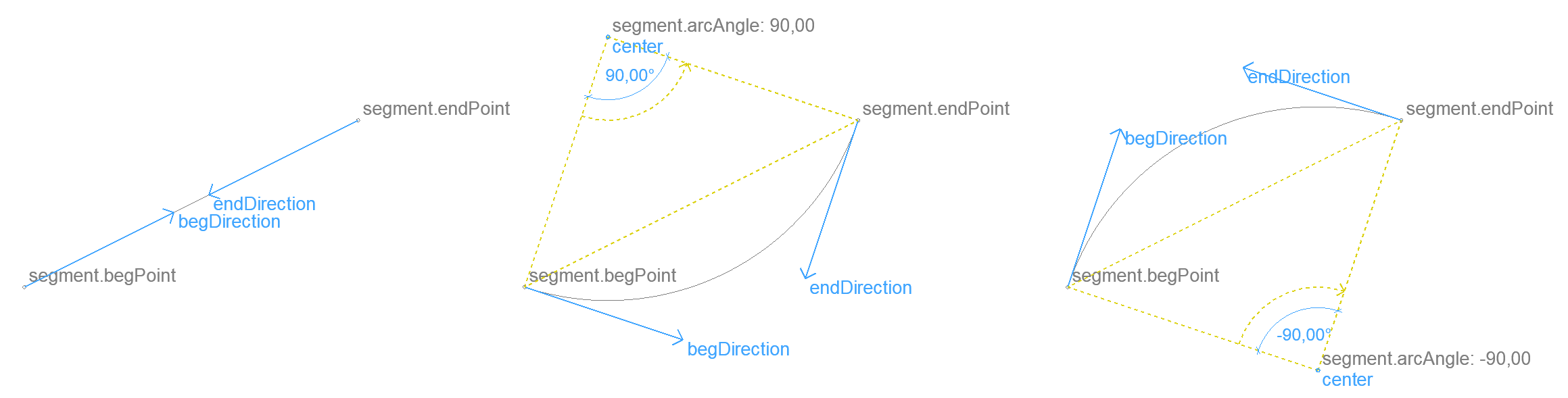
Direction vectors of segment end points – 2D
Returns the tangents of the segment at the ends, pointing towards the other end.
When the segment is curved, the centerpoint of the arc is returned too.
Input
segment
.begPoint .endPoint
.x .y
.type (int) 0 - straight, 1 - curved
? .arcAngle Central angle of arc, needed only for curved segment
arcAngle = 0 gives an error, abs(arcAngle) > 360 gives bad results.
Result
begDirection tangential direction at beginning point towards endpoint
.ux .uy
? .is0 (bool)
endDirection tangential direction at endpoint towards beginning point
.ux .uy
? .is0 (bool)
center
.x .y
center is (0, 0) for straight segments.
begDirection and endDirection are null vectors when the segment ends are closer than 0.00000001 (1 / 100 000 mm). The key is0 only exists in this case.
Code snippet
dict _begDirection, _endDirection, _center call "BasicGeometry" parameters iFunction = BasicGeometry.DIRECTION_SEGMENT_2D, segment = _segment, returned_parameters _begDirection, _endDirection, _center
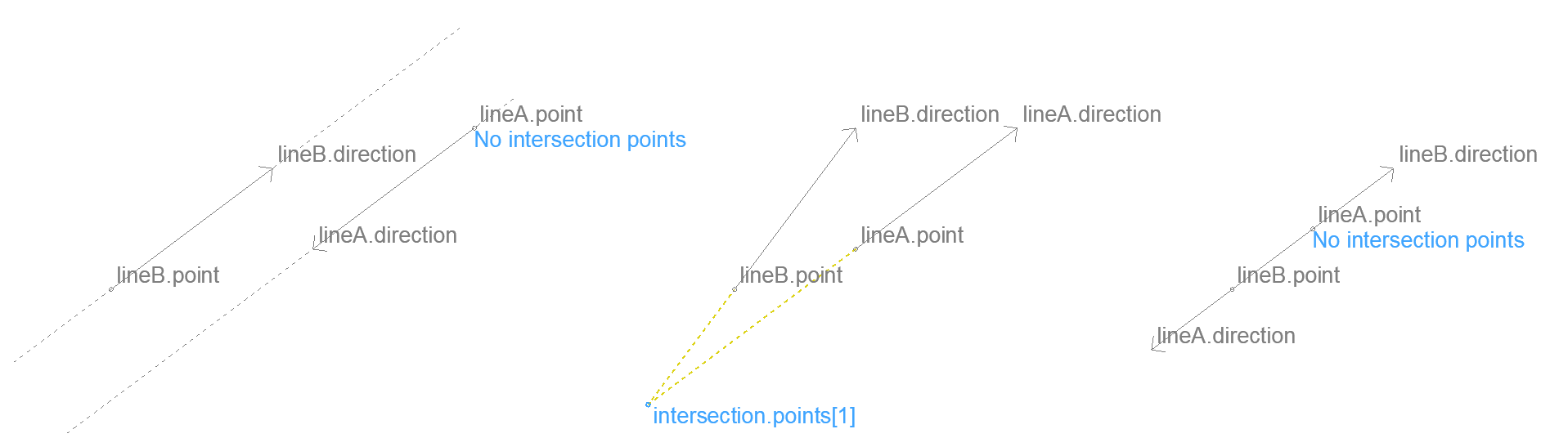
Intersection of two lines – 2D
Returns the intersection point of two infinite lines.
When the segment is curved, the centerpoint of the arc is returned too.
Input
lineA lineB
.direction
.ux .uy
.point
.x .y
Result
intersection
.points[]
.x .y
intersection.points array size is 1 if there is an intersection, 0 if the lines are parallel or are the same. When the angle between the lines is smaller than 0.0081° (1/10 mm divergence over 1 m) they are considered parallel.
An empty array is returned when any of the input direction vectors is a null vector. The key is0 only exists in this case.
Code snippet
dict _intersection call "BasicGeometry" parameters iFunction = BasicGeometry.INTERSECT_LINE_LINE_2D, lineA = _lineA, lineB = _lineB, returned_parameters _intersection
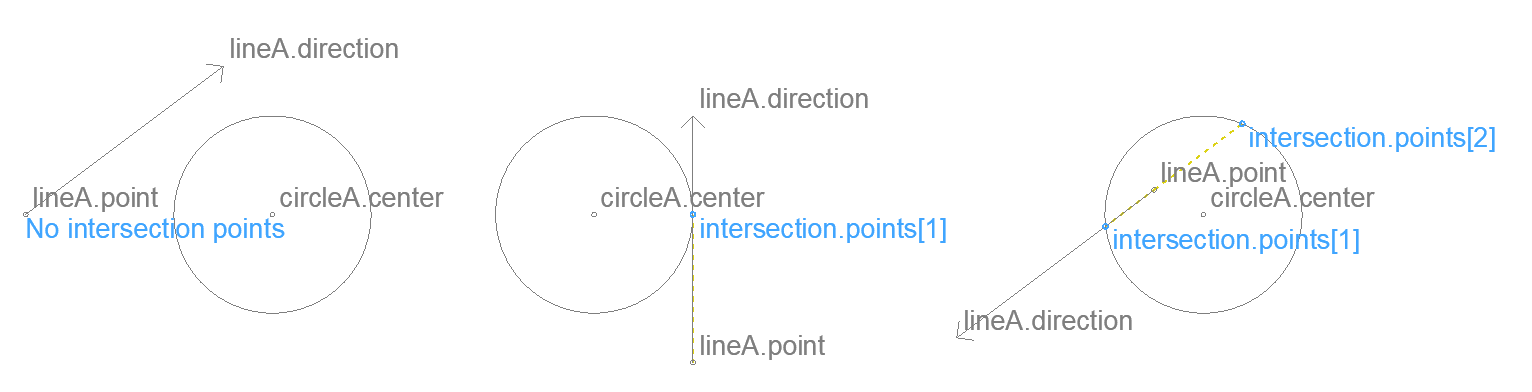
Intersection of a circle and a line – 2D
Returns the intersection points of a circle and an infinite line.
Input
lineA
.direction
.ux .uy
circleA
.center
.x .y
.radius
Result
intersection
.points[]
.x .y
intersection.points array size is 2 when the line goes through the circle, 1 when it is tangential.
Tangential lines are detected with a precision of 1/10 mm. When circleA.radius is smaller than 1/10 mm and the line goes through the circle, only 1 point is returned.
An empty array is returned when there are no intersections.
Code snippet
dict _intersection call "BasicGeometry" parameters iFunction = BasicGeometry.INTERSECT_CIRCLE_LINE_2D, circleA = _circleA, lineA = _lineA, returned_parameters _intersection
Intersection of a segment and a line – 2D
Returns the intersection points of a segment and an infinite line.
Input
lineA
.direction
.ux .uy
.point
.x .y
segment
.begPoint .endPoint
.x .y
.type (int) 0 - straight, 1 - curved
? .arcAngle Central angle of arc, needed only for curved segment
arcAngle = 0 gives an error, abs(arcAngle) > 360 gives bad results.
Result
intersection
.points[]
.x .y
.tangent tangent of segment at intersection
.ux .uy
The direction of the tangent of a curved segment is the radius from the arc center to the intersection rotated 90° counterclockwise.
The direction of the tangent of a straight segment is the direction of the segment from the beginning point to the endpoint.
When the segment is straight:
- When the angle between the segment and the line is smaller than 0.0081° (1/10 mm divergence over 1 m) they are considered parallel.
When it is curved:
- When the radius is smaller than 1/10 mm, no intersection is returned even if the line goes through the segment.
- No intersection is returned for a tangential line. Tangential position is detected with a precision of 1/10 mm.
Endpoints are detected with a precision of 1/10 mm.
Code snippet
dict _intersection call "BasicGeometry" parameters iFunction = BasicGeometry.INTERSECT_SEGMENT_LINE_2D, segment = _segment, lineA = _lineA, returned_parameters _intersection
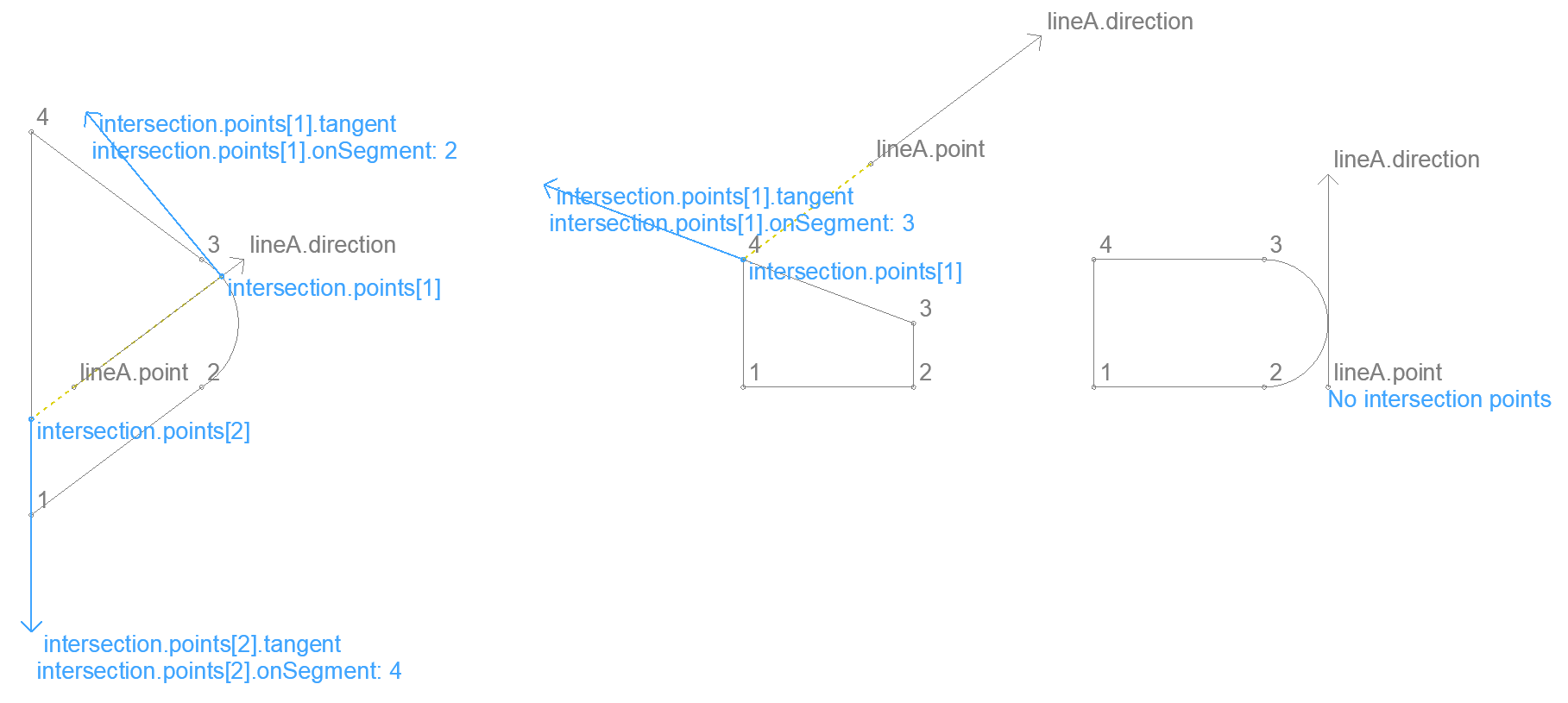
Intersection of a polygon and a line – 2D
Returns the intersection of a polygon and an infinite line.
Input
polygon
.contour
.edges[]
.begPoint
.x .y
.type (int) 0 - straight, 1 - curved
? .arcAngle Central angle of arc, needed only for curved edges
lineA
.direction
.ux .uy
.point
.x .y
Result
intersection
.points[]
.x .y
.onSegment (int) the index of the input edge the intersection is on
.tangent tangent of edge at intersection
.ux .uy
The results are calculated by intersecting the line with each edge as a segment. The same corner cases apply as written at Intersection of a segment and a line.
Intersections at a corner belong to only one edge. When an intersection is close to the beginning of an edge (with 1/10 mm precision), onSegment points to the previous edge.
Intersections closer than 1/10 mm are returned only once. This can happen with extremely narrow polygons.
Code snippet
dict _intersection call "BasicGeometry" parameters iFunction = BasicGeometry.INTERSECT_LINE_POLYGON_2D, polygon = _polygon, lineA = _lineA, returned_parameters _intersection
Insert a point onto a segment at given distance from start – 2D
Returns a point that is at the given distance on a segment. When the segment is curved, distance is measured along the arc.
Input
segment
.begPoint .endPoint
.x .y
.type (int) 0 - straight, 1 - curved
? .arcAngle Central angle of arc, needed only for curved segment
insertionDist (real) distance
insertionDist can be negative, or longer than the segment length: the resulting point will be outside the segment (along the same line or circle).
The segment endpoints have to be different, otherwise the results are incorrect.
Result
inserted
.point
.x .y
.angle arcAngle of the part of the input segment from the beginning point to the inserted point
inserted.angle can be greater than 360° when insertionDist is larger than the length of a full circle along the arc.
inserted.angle is 0 when the input segment is straight.
Code snippet
dict _inserted call "BasicGeometry" parameters iFunction = BasicGeometry.INSERT_POINT_TO_SEGMENT_2D, segment = _segment, insertionDist = insertionDist, returned_parameters _inserted
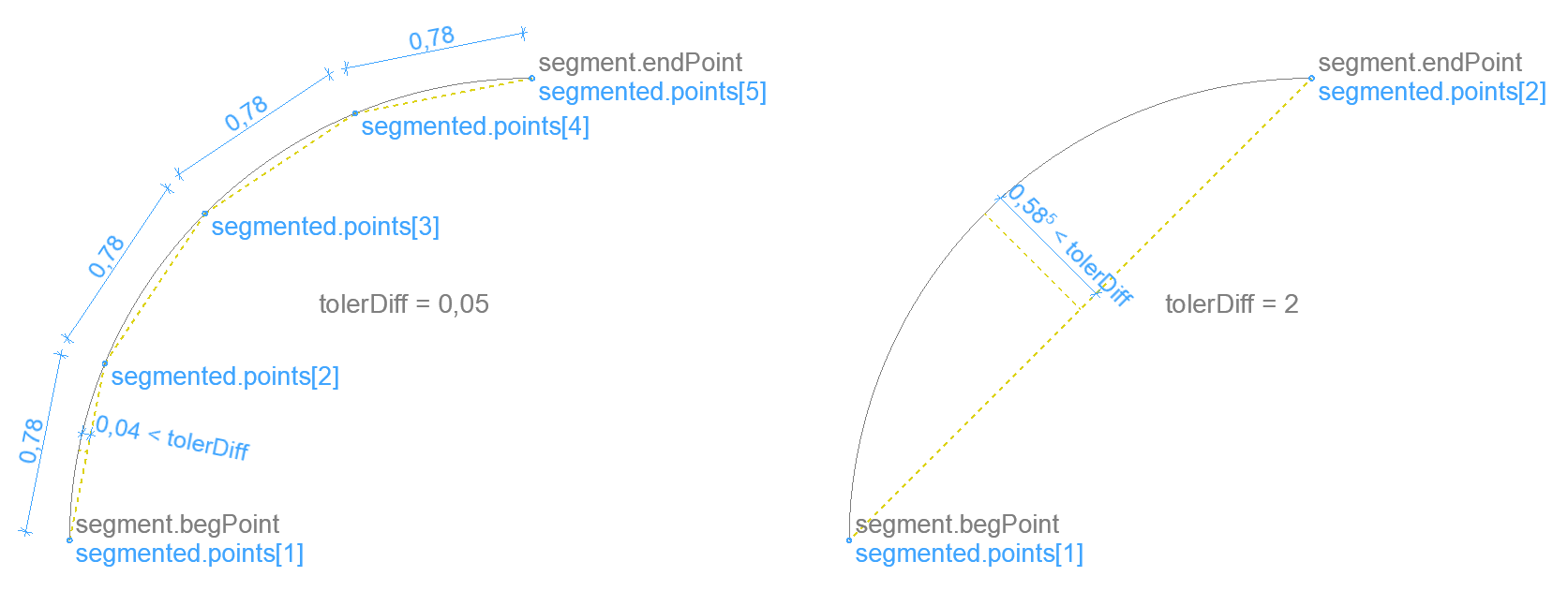
Segmentation of an arc with given tolerance – 2D
Divides an arc evenly, so that the greatest distance of the chord between two neighboring points and the arc is less than a given length (similar to the TOLER command).
Input
segment
.begPoint .endPoint
.x .y
.type (int) 0 - straight, 1 - curved
.arcAngle Central angle of arc
tolerDiff (real) tolerance
When tolerDiff is smaller than 1/10 mm, it will be used with the value 1/10 mm. Setting tolerDiff larger than the radius of the arc will return the two endpoints.
The segment endpoints have to be different, otherwise the results are bad.
Result
segmented
.points[]
.x .y
Altough segment.type = 0 (straight) is allowed as input, there is no point to call this function on a straight segment. The result will be an empty array.
inserted.angle is 0 when the input segment is straight.
Code snippet
dict _segmented call "BasicGeometry" parameters iFunction = BasicGeometry.SEGMENT_ARC_2D, segment = _segment, tolerDiff = tolerDiff, returned_parameters _segmented
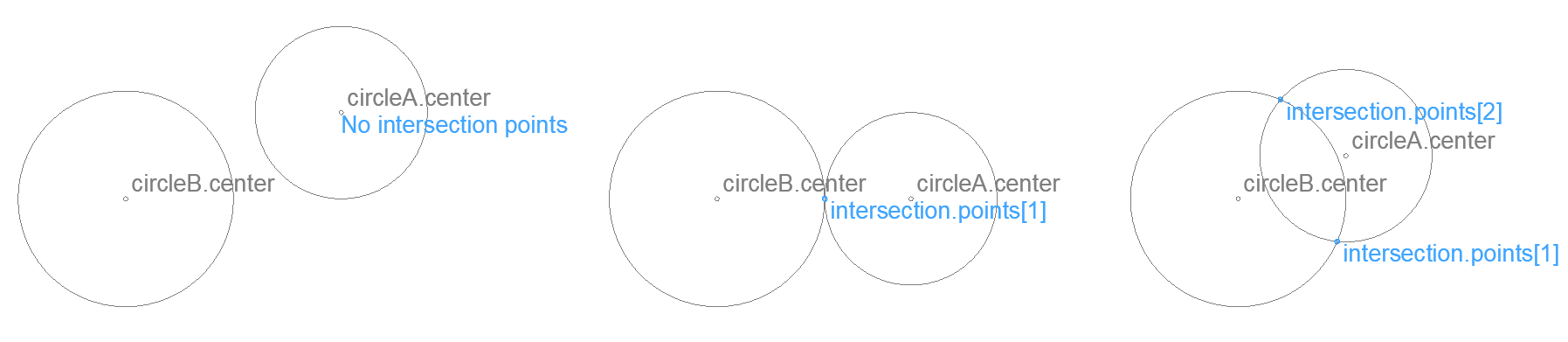
Intersection of two circles – 2D
Returns the intersection points of two circles.
Input
circleA
.center
.x .y
.radius
circleB
.center
.x .y
.radius
Result
intersection
.count (int) number of valid intersections - 0, 1 or 2
.points[2] always two entries, some of which might be invalid
.x .y
Use intersection.points[] array elements only up to intersection.count, others are invalid.
Circles with equal radius and closer than 1/10 mm are considered the same, no intersection is returned.
Tangential circle positions are calculated with an accuracy of 1/10 mm.
Code snippet
dict _intersection call "BasicGeometry" parameters iFunction = BasicGeometry.INTERSECT_CIRCLE_CIRCLE_2D, circleA = _circleA, circleB = _circleB, returned_parameters _intersection
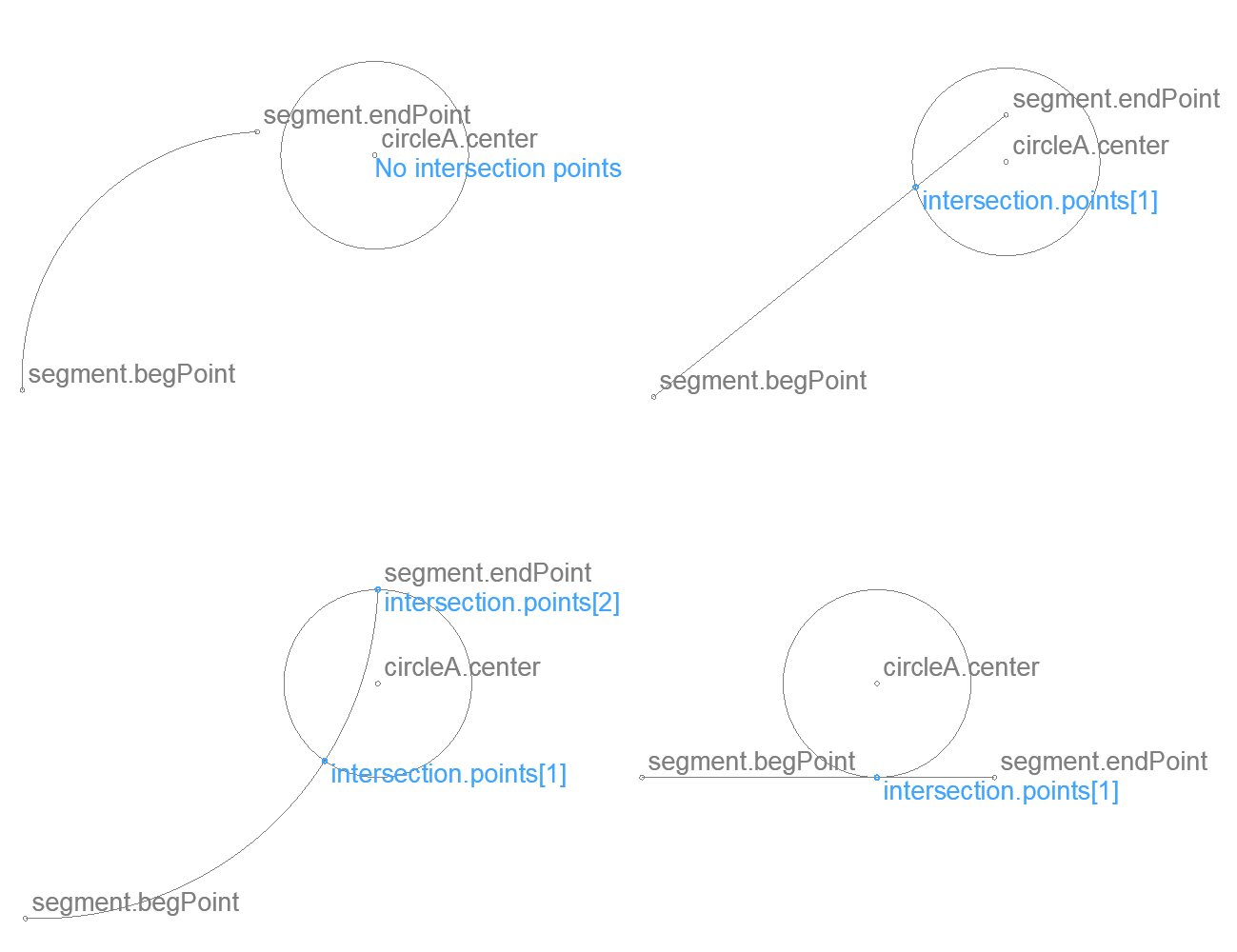
Intersection of a segment and a circle – 2D
Returns the intersection points of a segment and a circle.
Input
segment
.begPoint .endPoint
.x .y
.type (int) 0 - straight, 1 - curved
? .arcAngle Central angle of arc, needed only for curved segment
circleA
.center
.x .y
.radius
Result
intersection
.points[]
.x .y
When the segment is straight, corner cases written at Intersection of a circle and a line apply.
When the segment is curved, corner cases written at Intersection of two circles apply.
Endpoints, tangential positions are detected with a precision of 1/10 mm.
intersection.points array size is the number of found intersections.
Code snippet
dict _intersection call "BasicGeometry" parameters iFunction = BasicGeometry.INTERSECT_SEGMENT_CIRCLE_2D, segment = _segment, circleA = _circleA, returned_parameters _intersection
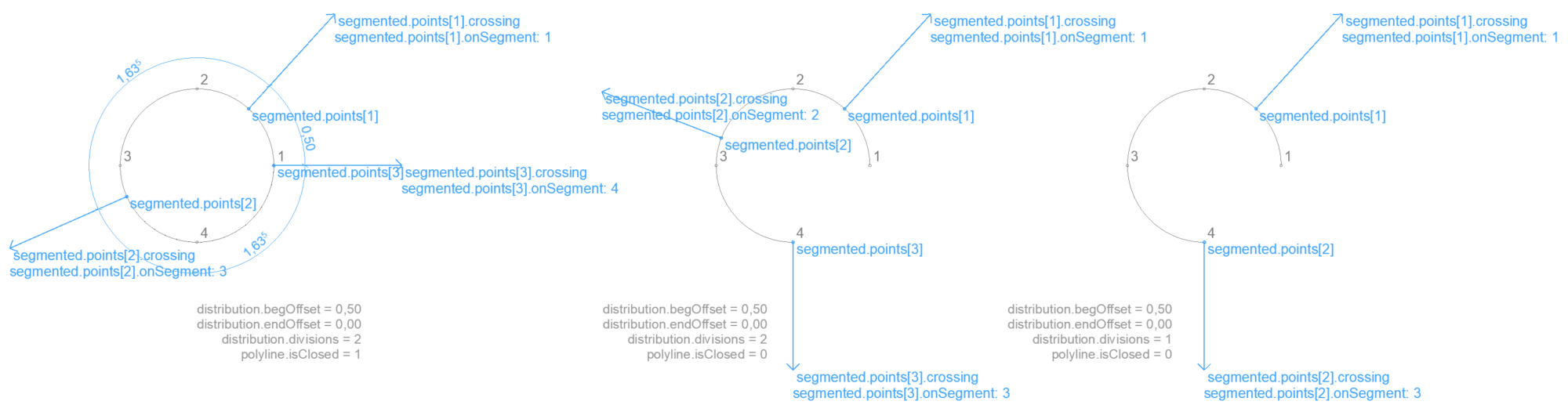
Distribute points evenly on polyline – 2D
Returns points that are evenly distributed on a polyline. It is possible to define offsets at the two ends of the polyline that are cut off from the distribution.
Input
polyline
.isClosed (bool) The polyline is closed (last edge ends at the first edge's begPoint)
.contour
.edges[]
.begPoint
.x .y
.type (int) 0 - straight, 1 - curved
? .arcAngle Central angle of arc, needed only for curved edges
distribution
.begOffset
.endOffset
.divisions Divide polyline into this # of parts. For example 2 returns 3 points.
distribution.divisions should be greater than 0. For practical use it should be an integer.
With distribution.divisions = 1 offsets from both ends of the polyline are returned.
The distribution offsets are used with their absolute value. When the sum of the two offsets is longer than the polyline, no points are returned.
Result
segmented
.points[]
.x .y
.onSegment (int) Index of the input polyline edge on which the point is.
.crossing Direction vector perpendicular to the polyline at the point.
.ux .uy
Points near a corner belong to the edge ending there (with 1/10 mm precision).
crossing direction is always pointing to the right side of the polyline (looking in the direction of the polyline).
Code snippet
dict _segmented call "BasicGeometry" parameters iFunction = BasicGeometry.DISTRIBUTION_POLYLINE_2D, polyline = _polyline, distribution = _distribution, returned_parameters _segmented
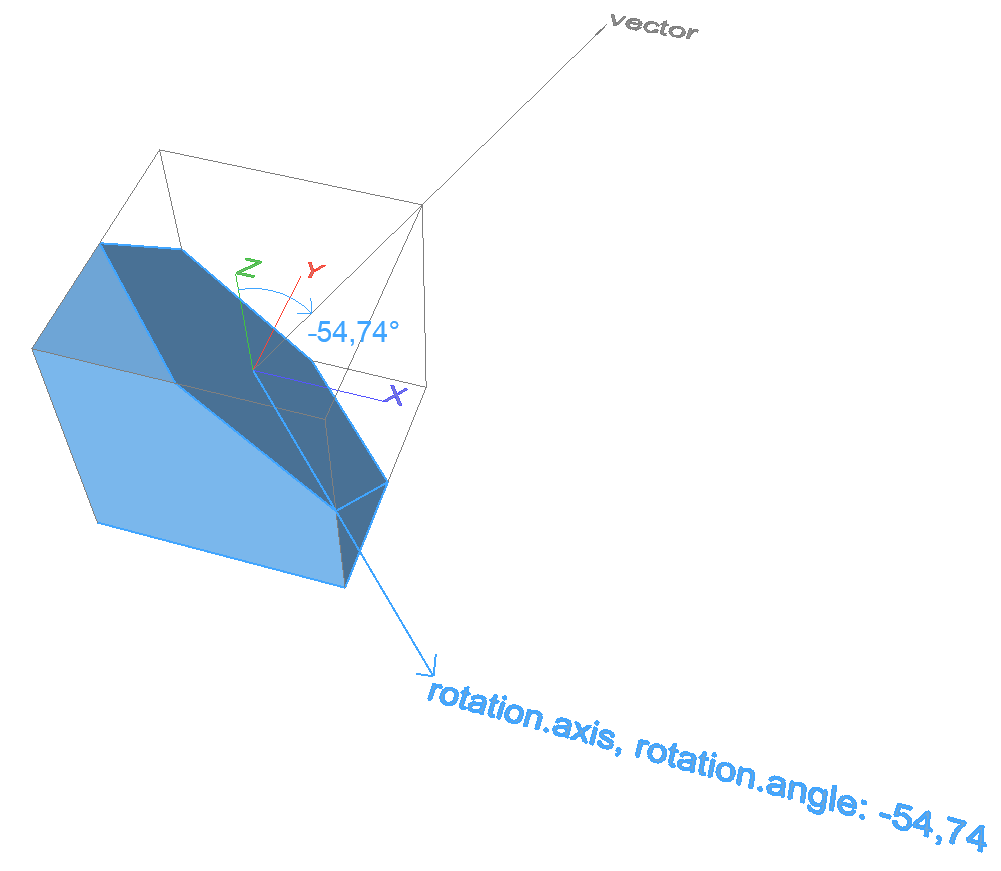
Align Z with vector – 3D
Returns the necessary rotation axis and angle that rotates the Z axis to be parallel with the input vector.
Input
vector
.dx .dy .dz
The input vector’s length should be greater than 0.
Result
rotation
.axis direction vector of rotation axis
.dx .dy .dz
.angle necessary rotation around .axis, degrees
Code snippet
dict _rotation call "BasicGeometry" parameters iFunction = BasicGeometry.ROT_Z_TO_VECTOR_3D, vector = _cutPlaneNormal, returned_parameters _rotation
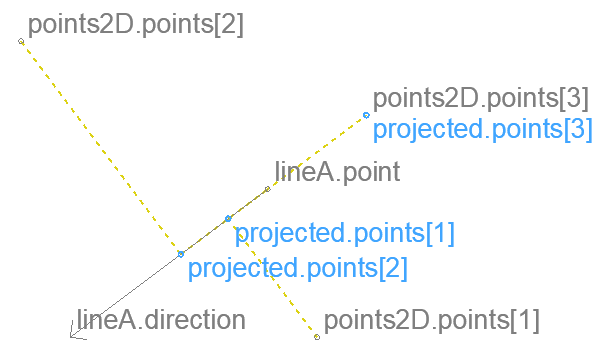
Project points onto line – 2D
Projects points perpendicularly onto a line.
Input
lineA
.point point on line
.x .y
.direction direction vector parallel with line
.ux .uy
points2D
.points[]
.x .y
points2D.points[] array size has to be at least 1.
Result
projected
.points[]
.x .y
projected.points[] array has the same number of elements as input points2D.points[] array.
Code snippet
dict _projected call "BasicGeometry" parameters iFunction = BasicGeometry.PROJECT_POINTS_LINE_2D, points2D = _points2D, lineA = _lineA, returned_parameters _projected
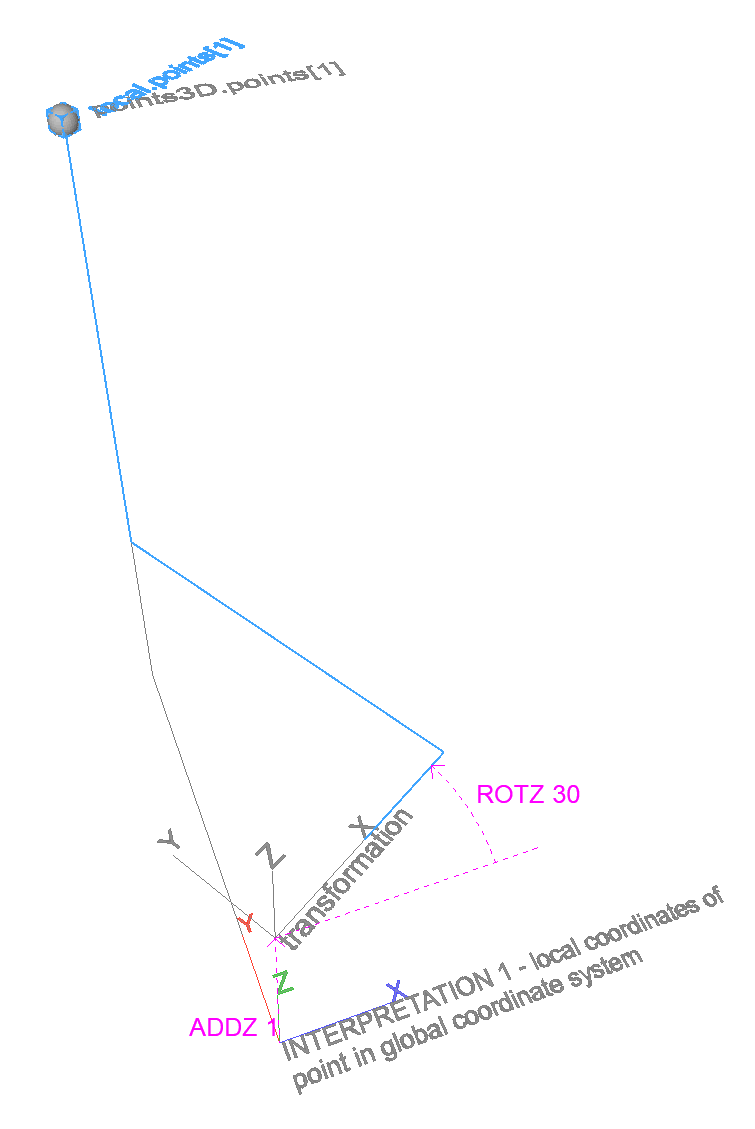
Transform points – 3D
Returns the coordinates of local points expressed in a global coordinate system.
Can be used to calculate global coordinates of points in a local coordinate system described by an XFORM-style transformation matrix (global coordinates of points placed in transformed coordinate system).
Can be used to transform points with an XFORM-style transformation matrix, returning the coordinates after the transformation.
Input
points3D
.points[]
.x .y .z
transformation
.origin origin after the transformation
.x .y .z
.XAxis vector of transformed X axis, relative to transformed origin
.dx .dy .dz
.YAxis vector of transformed Y axis, relative to transformed origin
.dx .dy .dz
.ZAxis vector of transformed Z axis, relative to transformed origin
.dx .dy .dz
points3D must contain at least an empty points[] array.
Result
global
.points[]
.x .y .z
global.points[] array has the same number of elements as input points3D.points[] array.
Code snippet
dict _global
call "BasicGeometry" parameters iFunction = BasicGeometry.LOCAL_POINTS_TO_GLOBAL_3D,
transformation = _transformation,
points3D = _points3D,
returned_parameters _global
There are two ways to visualize the operation:
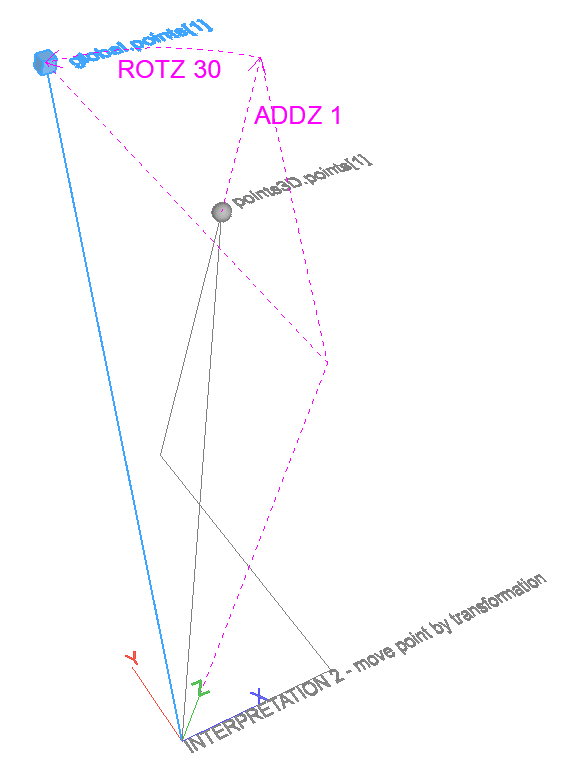
- Global coordinates of a point that was modeled in a transformed coordinate system. The point is fixed in space, the coordinate system of the result is transformed by the inverse if the input transformation.

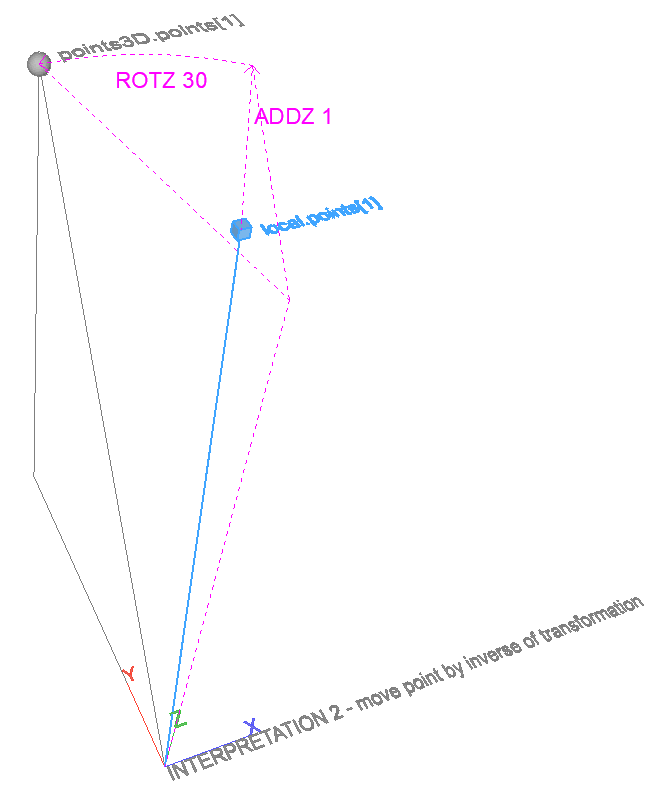
Inverse-transform points – 3D
Returns the coordinates of global points expressed in a local coordinate system.
Can be used to calculate local coordinates of points in the global coordinate system. The local coordinate system is described by an XFORM-style transformation matrix (local coordinates of points placed in the global coordinate system).
Can be used to transform points with the inverse of a transformation matrix, returning the coordinates before the transformation.
Input
points3D
.points[]
.x .y .z
transformation
.origin origin after the transformation
.x .y .z
.XAxis vector of transformed X axis, relative to transformed origin
.dx .dy .dz
.YAxis vector of transformed Y axis, relative to transformed origin
.dx .dy .dz
.ZAxis vector of transformed Z axis, relative to transformed origin
.dx .dy .dz
points3D must contain at least an empty points[] array.
Result
local
.points[]
.x .y .z
local.points[] array has the same number of elements as input points3D.points[] array.
Code snippet
dict _local
call "BasicGeometry" parameters iFunction = BasicGeometry.GLOBAL_POINTS_TO_LOCAL_3D,
transformation = _transformation,
points3D = _points3D,
returned_parameters _local
There are two ways to visualize the operation:
- Local, transformed coordinates of a point that was modeled in the global coordinate system. The point is fixed in space, the coordinate system of the result is transformed.
- Undo transformations on a point. The coordinate system is fixed, the point is transformed by the inverse of the input transformation.
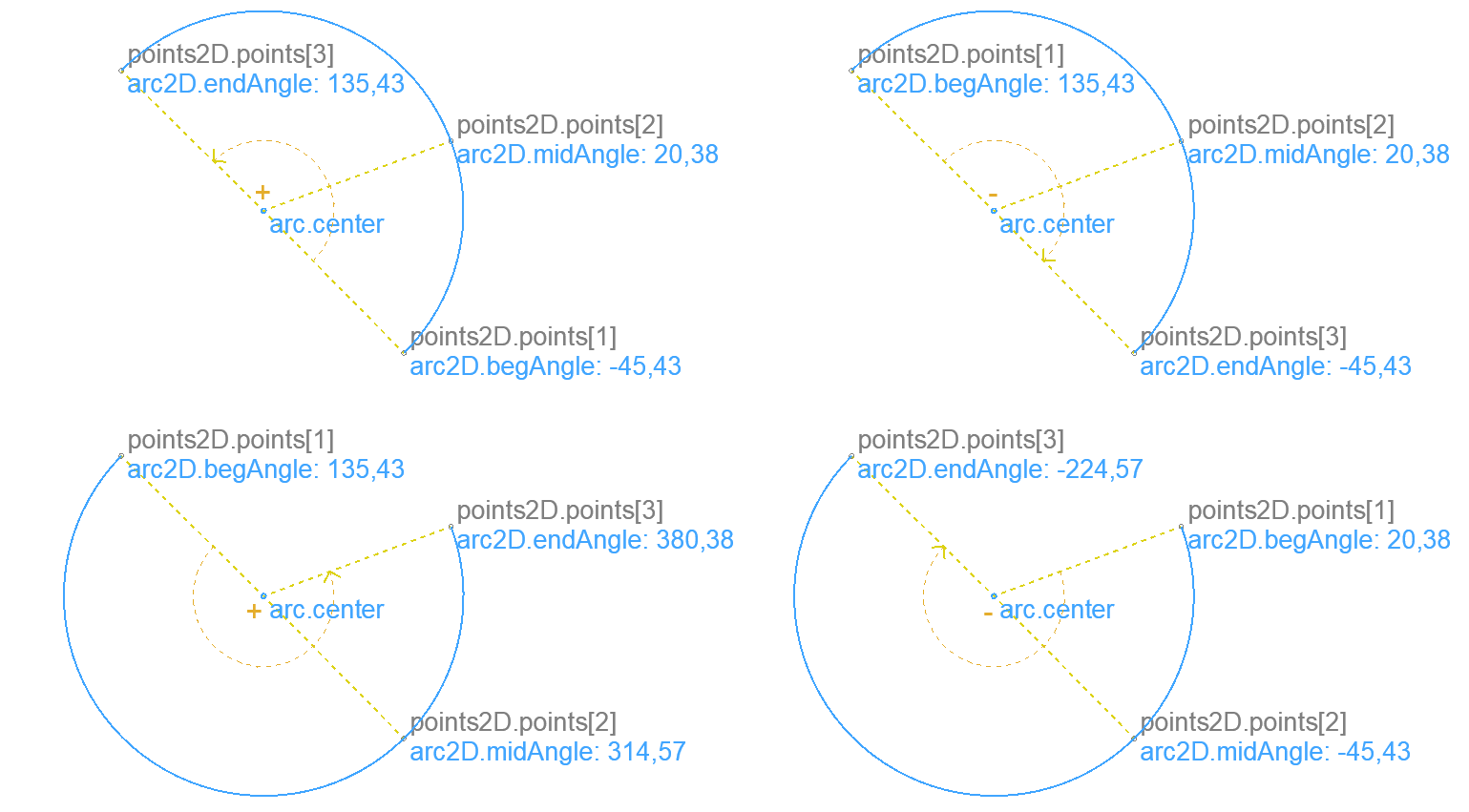
Arc through three points in order – 2D
Returns an arc that goes through the input points in order. Returns the polar angle of the input points relative to the X-axis.
Input
points2D
.points[3] three points in order: beginning, intermediate, end
.x .y
Result
arc2D
.exists (bool) Is there a valid solution?
.radius radius of circle through input points
.center center of circle
.x .y
.begAngle polar angle of beginning point
.midAngle polar angle of intermediate point
.endAngle polar angle of end point
A valid solution doesn’t exist when any two of the input points are the same, or all three of them lie on the same line.
The returned polar angles are ordered ( sgn(begAngle - midAngle) = sgn(midAngle - endAngle) ). Their absolute value can be larger than 360°, their value can be lower than 0°. The absolute value of the difference between two angles is always less than 360°. This means the relative angle between any two points can be easily passed to GDL polygon commands using status code 4000.
Code snippet
dict _arc
call "BasicGeometry" parameters iFunction = BasicGeometry.ARC_THROUGH_POINTS_2D,
points2D = _points2D,
returned_parameters _arc
Project points onto circle from inside – 2D
Project points onto circle from a point inside the circle.
Input
points2D
.points[]
.x .y
pointFrom
.x .y
circleA
.center
.x .y
.radius
pointFrom should be a point inside the circle.
points2D.points[] can be anywhere in the plane except pointFrom.
Result
projected
.points[]
.x .y
Each input point will have exactly one corresponding projected point. Input points that are the same as pointFrom are returned unchanged.
An empty projected.points[] array is returned when pointFrom wasn’t inside the circle.
Code snippet
dict _projected
call "BasicGeometry" parameters iFunction = BasicGeometry.PROJECT_POINTS_CIRCLE_INNER_2D,
points2D = _points2D,
pointFrom = _pointFrom,
circleA = _circleA,
returned_parameters _projected