ADDX

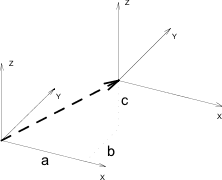
ADDX dx

ADDY

ADDY dy

ADDZ

ADDZ dz

Moves the local coordinate system along the given axis by dx, dy or dz respectively.

ADD

ADD dx, dy, dz

Replaces the sequence ADDX dx: ADDY dy: ADDZ dz.

Example:

ADD a, b, c

It has only one entry in the stack, thus it can be deleted with DEL 1.

MULX

MULX mx

MULY

MULY my

MULZ

MULZ mz

Scales the local coordinate system along the given axis. Negative mx, my, mz means simultaneous mirroring.

MUL

MUL mx, my, mz

Replaces the sequence MULX mx: MULY my: MULZ mz. It has only one entry in the stack, thus it can be deleted with DEL 1.

ROTX

ROTX alphax

ROTY

ROTY alphay

ROTZ

ROTZ alphaz

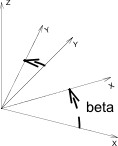
Rotates the local coordinate system around the given axis by alphax, alphay, alphaz degrees respectively, counterclockwise.

Example:

ROTZ beta

ROT

ROT x, y, z, alpha

Rotates the local coordinate system around the axis defined by the vector (x, y, z) by alpha degrees, counterclockwise.
It has only one entry in the stack, thus it can be deleted with DEL 1.

XFORM

XFORM newx_x, newy_x, newz_x, offset_x,
      newx_y, newy_y, newz_y, offset_y,
      newx_z, newy_z, newz_z, offset_z

Defines a complete transformation matrix. It is mainly used in
automatic GDL code generation. It has only one entry in the stack.

x’ = newx_x * x + newy_x * y + newz_x * z + offset_x

y’ = newx_y * x + newy_y * y + newz_y * z + offset_y

z’ = newx_z * x + newy_z * y + newz_z * z + offset_z

Example code:

A = 60
B = 30
XFORM 2, COS(A), COS(B)*0.6, 0,
      0, SIN(A), SIN(B)*0.6, 0,
      0, 0, 1, 0
BLOCK 1, 1, 1

… and it’s 3D view: